[Theory.1] Vector Analysis
벡터해석
전자기학을 공부하기 위해선 벡터를 해석할 줄 알아야합니다. 전자기학 뿐만 아니라 벡터는 모든 개념에서 기초가 되므로 간단하게 짚고 넘어가며 알아보겠습니다. 자세한 내용은 관련 서적을 참고하시면 좋습니다.
벡터대수
벡터연산
벡터란 방향을 내포하는 개념이므로 크기를 계산할 때 변위(displacement) 로 바라봅니다. 방향성을 제거했을 때는 스칼라(scalar) 입니다. 간단한 예시를 보겠습니다.
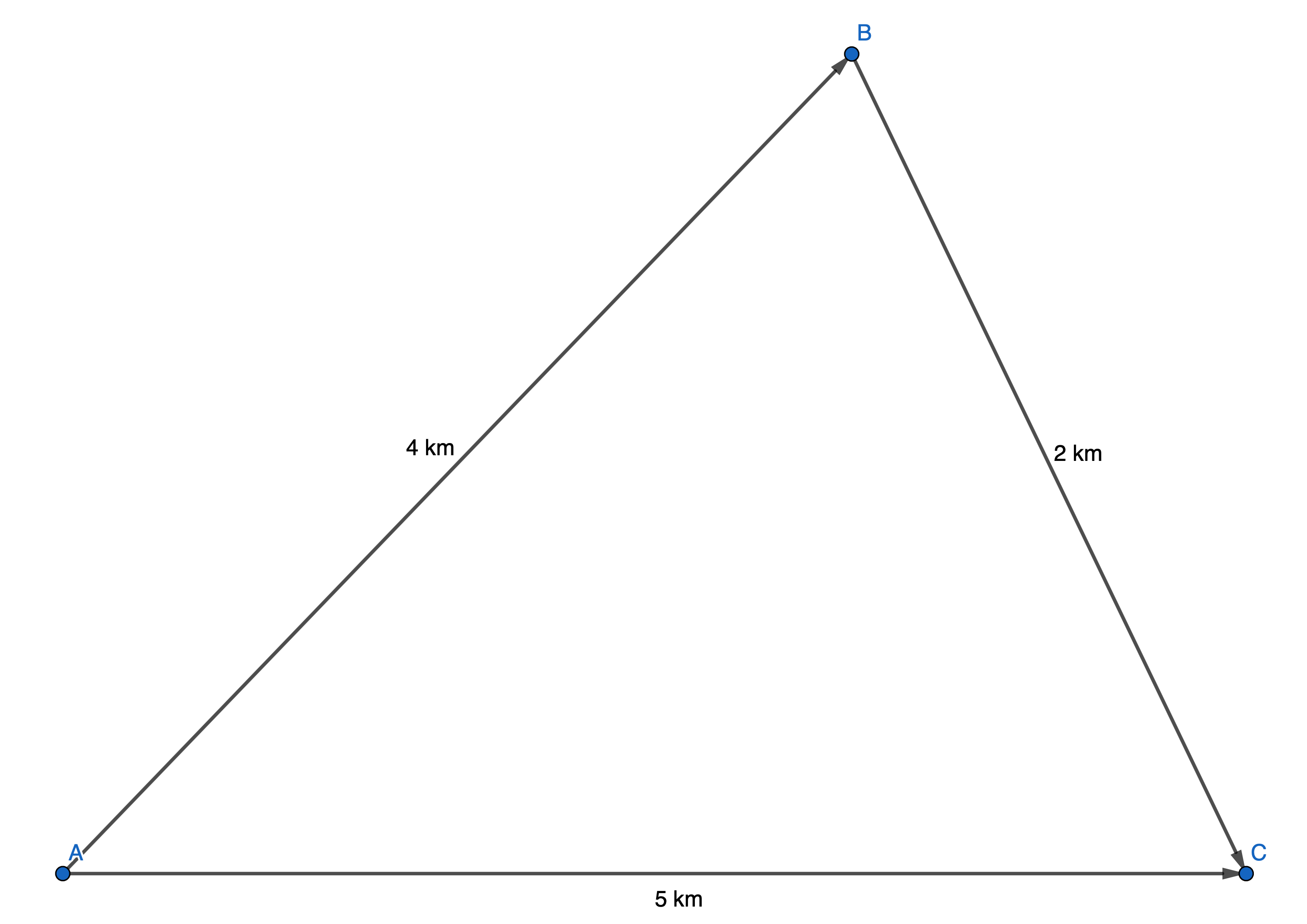
[Figure. 1]을 보겠습니다. 만약 점 A 출발해서 점 B 를 지나 점 C에 도착한다면, 변위는 5 \((km)\) 가 되고 이동거리, 즉 스칼라는 6 \((km)\) 가 됩니다. 그렇다면 벡터를 연산할 때는 어떨까요.
- 두 벡터의 덧셈과 뺄셈
- 스칼라곱셈
- 점곱
벡터의 덧셈은 화살표의 머리와 꼬리를 이어준다는 느낌입니다. 이때, 덧셈의 순서는 바꿔도 무방합니다.(교환법칙). [Figure. 2]는 두 개의 벡터 \(\vec{a}\) 와 \(\vec{b}\)를 보여줍니다.
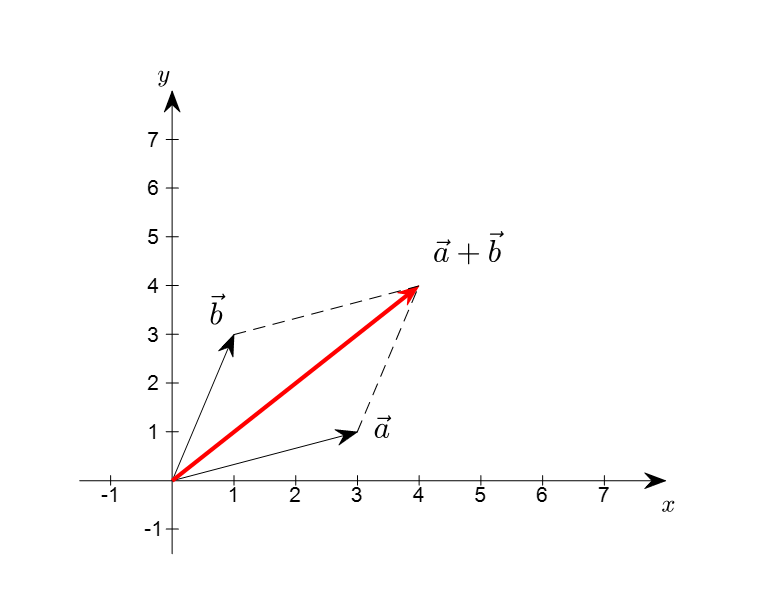
만일, 벡터 \(\vec{c}\) 를 추가하여 3개의 벡터를 계산한다면 결합법칙이 성립합니다.
\[(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) \tag{1}\]어떤 벡터를 뺄려면 그 벡터의 반대방향인 벡터를 더해주면 됩니다.
\[\vec{a} - \vec{b} = \vec{a} + (-\vec{b}) \tag{2}\]스칼라 곱셈(scalar multiplication)은 벡터의 크기와 방향을 바꿔줍니다. 만일, 임의의 스칼라 \(\alpha\) 값이 양수면 방향은 유지한 상태로 크기가 변하고 음수값이면 방향이 반대가 됩니다. 이때, 분배법칙이 성립한다.
\[\alpha(\vec{a} + \vec{b}) = \alpha \vec{a} + \alpha \vec{b} \tag{3}\]점곱(dot product or inner product)은 벡터에서 방향성을 제거하고 크기만 볼 것입니다. 다른 말로는 내적 혹은 스칼라 곱이라고 합니다. 이때 교환법칙과 분배법칙이 성립됩니다.
\[\begin{align*} \vec{a} \cdot \vec{b} & \equiv \; \vec{a} \; \vec{b} \; cos\theta \\ \vec{a} \cdot \vec{b} &= \vec{b} \cdot \vec{a} \\ \vec{a} \cdot (\vec{b} + \vec{c}) &= \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} \tag{4} \\ \end{align*}\]위 성질을 만족하므로 만일 두 벡터 \(\vec{a}\) 와 \(\vec{b}\) 의 방향이 나란하다면, \(\vec{a} \cdot \vec{b} = ab\) 이고 수직이면 \(\vec{a} \cdot \vec{b} = 0\) 모든 벡터에 대해 \(\vec{a} \cdot \vec{a} = a^2\) 를 만족합니다.
성분형식
벡터를 기술할 때는 기준이 되는 좌표가 있어야 합니다. 일반적으로 접하신 직각좌표게에선 직각좌표 성분을 사용하여 계산합니다. 3차원 직각좌표계의 \(x, y, z\) 축에 나란한 단위벡터를 \(\hat{x}, \hat{y}, \hat{z}\) 로 한다면 이를 바탕벡터 혹은 기저벡터 (basis vector)라고 하며 다음과 같이 임의의 벡터를 표현할 수 있습니다.
\[\textbf{a} = a_x\hat{x} + a_y\hat{y} + a_z\hat{z} \tag{5}\]
위와 같이 벡터를 성분으로 표기할 수 있습니다. 이제, 앞서 언급한 벡터 연산을 성분으로 계산할 수 있습니다.
벡터를 곱할 때 내적의 형태로 스칼라곱을 해왔습니다. 벡터에는 곱셈에서 내적과 외적의 개념이 분리되어 있으며 이번엔 외적에 대해 알아보겠습니다. 외적은 내적과 달리 방향성을 내포합니다. 그렇기에 곱하는 순서와 기저벡터의 관계에 따라 값이 달라집니다.
\[\begin{align*} \\ \textbf{A} \times \textbf{B} &= (A_x\hat{x} + A_y\hat{y} + A_z\hat{z}) \; \times \; (B_x\hat{x} + B_y\hat{y} + B_z\hat{z}) \\ &= (A_y B_z - A_z B_z)\hat{x} + (A_z B_x - A_x B_z)\hat{y} + (A_x B_y - A_y B_x)\hat{z} \tag{10} \\ \end{align*}\]위 과정은 단위벡터 사이의 관계를 통해 적을 수 있습니다. 자세한 과정은 생략하였습니다. 위 식을 행렬로 적으면 다음과 같습니다.
\[\begin{equation*} \textbf{A} \times \textbf{B} = \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \\ \end{vmatrix} \end{equation*} \tag{11}\]삼중곱
삼중곱은 두 경우로 나눠집니다. 스칼라 삼중곱과 벡터 삼중곱입니다.
먼저 스칼라 삼중곱을 알아보겠습니다. 대표적인 예시로는 평행육면체의 부피를 구하는 경우와 같습니다. \(\vert \textbf{A} \cdot (\textbf{B} \times \textbf{C})\vert\) 는 바닥면의 넓이 \(\vert \textbf{B} \times \textbf{C} \vert\) 에 높이 \(\vert \textbf{A} cos\theta \vert\)를 곱한것과 같습니다.
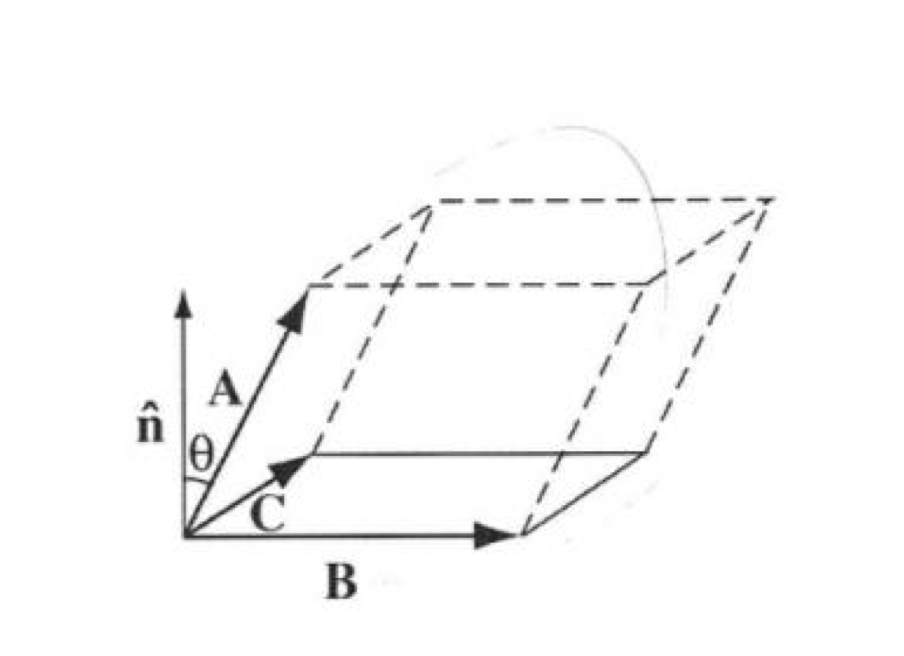
[Figure. 4]는 책에 기재된 그림입니다. 위와 같이 스칼라 삼중곱을 표현하면 다음과 같습니다.
\[\textbf{A} \cdot (\textbf{B} \times \textbf{C}) = \textbf{B} \cdot (\textbf{C} \times \textbf{A}) = \textbf{C} \cdot (\textbf{A} \times \textbf{C}) \tag{12}\]위 식을 좌표성분으로 표현하면 다음과 같습니다.
\[\begin{equation*} \textbf{A} \cdot (\textbf{B} \times \textbf{C}) = \begin{vmatrix} A_x & A_y & A_z \\ B_x & B_y & B_z \\ C_x & C_y & C_z \\ \end{vmatrix} \end{equation*} \tag{13}\]다음으로 벡터 삼중곱에 대해 알아보겠습니다. \(\textbf{A} \times (\textbf{B} \times \textbf{C})\) 같은 꼴은 BAC-CAB 규칙을 사용합니다.(저는 백캡이라 부릅니다.)
\[\textbf{A} \times (\textbf{B} \times \textbf{C}) = \textbf{B}(\textbf{A} \cdot \textbf{C}) - \textbf{C}(\textbf{A} \cdot \textbf{B}) \tag{14}\]앞서 말했듯이 백터의 외적은 방향성을 지니므로 곱하는 순서에 유의해야합니다.
위치, 변위, 분리 벡터
직각좌표계에서 생각해봅시다. 원점(O)에서 임의의 점까지의 벡터를 위치벡터(position vector)라고 합니다.
\[\textbf{r} \equiv x\hat{x} + y\hat{y} + z\hat{z} \tag{15}\]이때, 벡터r의 크기는 원점까지의 거리가 됩니다.
\[r = \sqrt{x^2 + y^2 + z^2} \tag{16}\]저희는 기저벡터, 좌표벡터를 사용해왔습니다. 이는 기준으로부터 원하는 좌표축에 따른 단위벡터(unit vector)입니다. 그렇다면 임의의 벡터에 대해서도 단위벡터를 구할수가 있습니다.
\[\hat{r} = \frac{\textbf{r}}{r} = \frac{x\hat{x} + y\hat{y} + z\hat{z}}{\sqrt{x^2 + y^2 + z^2}} \tag{17}\]만약, 직각좌표계에서 임의의 방향으로 미소하게 변할 때, 즉 미분의 개념을 도입하기 위해 표현하는 방식으로 미소 변위 벡터(infinitesimal displacement vector)가 있습니다. 저희는 임의의 벡터 r에 대해서 아주 미세하게 변하는 것을 표현하고 싶습니다. 이때 미소변위는 dr을 써서 표현하지 않고 특별한 글자로 지정하는 것이 좋습니다. 책에 서술된 바와 같이 저는 dI를 도입하겠습니다.
\[d\textbf{I} = dx\hat{x} + dy\hat{y} + dz\hat{z} \tag{18}\]전기역학에서는 전하가 있는 원천점(source)와 전기장 혹은 자기장을 측정하는 관찰점 (field point)가 있습니다. 각 점의 관계를 보기 위해 저희는 분리 벡터(separation vector)을 도입합니다. (물론, 소스를 기준으로 삼아 좌표계를 도입하여도 됩니다. 다만, 기저벡터를 새롭게 설정해야 하므로 보통 직각좌표계를 사용합니다.)

마찬가지로, 해당 벡터 \(\boldsymbol{\xi}\) 의 단위벡터는 다음과 같이 쓸 수 있습니다.
\[\boldsymbol{\hat{\xi}} = \frac{\boldsymbol{\xi}}{\xi} = \frac{\textbf{r}-\textbf{r}^\prime}{\vert \textbf{r} - \textbf{r}^\prime \vert} \tag{20}\]저희는 직각좌표계로 설명해왔으므로 해당 좌표성분으로 표현하면 다음과 같습니다.
\[\boldsymbol{\xi} = (x - x^\prime)\boldsymbol{\hat{x}} + (y - y^\prime)\boldsymbol{\hat{y}} + (z - z^\prime)\boldsymbol{\hat{z}} \tag{21}\]벡터 변환규칙
그동안 직교좌표계를 이용하여 설명하였습니다. 만일, 좌표계를 변환하면 기저벡터를 똑같이 사용할 수 없습니다. 이제 벡터를 변환하는 방법을 알아보겠습니다.
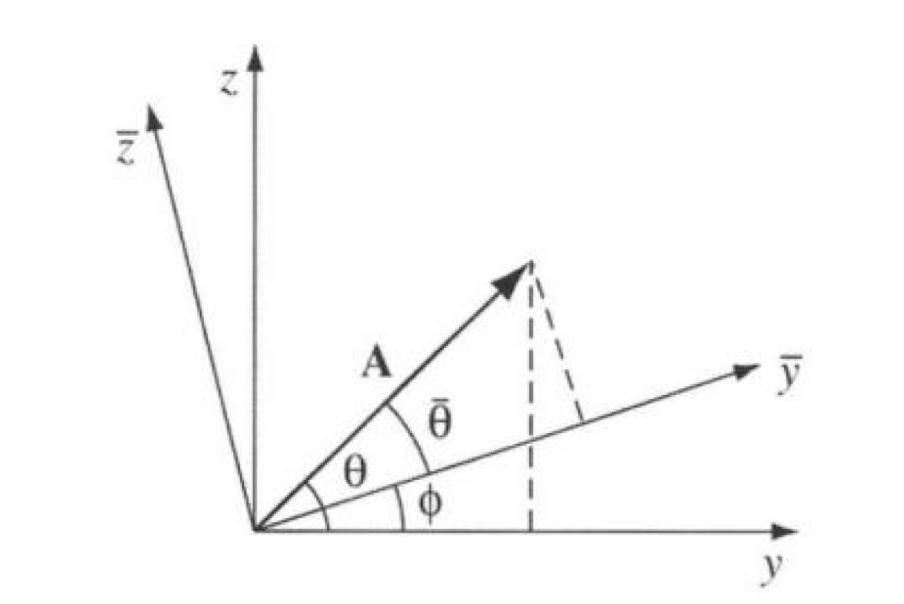
위 그림은 교재에서 가져왔습니다. y,z축인 2차원 좌표계를 \(\phi\) 만큼 양의 방향으로 회전시켰습니다. 회전한 좌표계에 대해 \(\bar{y}, \bar{z}\) 축으로 정의하겠습니다. 그렇다면 기존 벡터 A를 새로운 좌표계에 대해 표현하고자 합니다.
\[A_y = Acos\theta, \quad A_z = Asin\theta \tag{22}\]Eq.22는 기존벡터 A의 좌표성분입니다. 새로운 좌표계로 표현하면 다음과 같습니다.
\[\begin{align*} \bar{A}_y &=Acos\bar{\theta} =Acos(\theta-\phi) = A(cos\theta cos\phi + sin\theta sin\phi) \\ &=cos\phi A_y + sin\phi A_z , \end{align*}\] \[\begin{align*} \bar{A}_z &= Asin\bar{\theta} = Asin(\theta - \phi) = A(sin\theta cos\phi - cos\theta sin\phi) \\ &= -sin\phi A_y + cos\phi A_z \tag{23} \\ \end{align*}\]위 식을 3차원으로 확장해서 일반적인 행렬로 나타내면 다음과 같이 표현할 수 있습니다.
\[\begin{equation*} \begin{pmatrix} \bar{A}_x \\ \bar{A}_y \\ \bar{A}_z \\ \end{pmatrix} = \begin{pmatrix} R_{xx} & R_{xy} & R_{xz} \\ R_{yx} & R_{yy} & R_{yz} \\ R_{zx} & R_{zy} & R_{zz} \\ \end{pmatrix} \begin{pmatrix} A_x \\ A_y \\ A_z \\ \end{pmatrix} \end{equation*} \tag{24}\]재밌게도, 위 식을 한 줄로 적을 수 있습니다.
\[\bar{A}_i = \sum_{j=1}^3 R_{ij}A_j \tag{25}\]위 식에서 인덱스 \(i\)의 값 1,2,3은 각각 축을 의미합니다. 지금껏 직각좌표계에서 \(x,y,z\)를 사용했으니 \(i=1\)일때 \(x\)축이 됩니다.
좌표가 변할 때 벡터를 새롭게 표현할 수 있었습니다. 재밌는 점은 텐서(tensor)란 개념이 존재합니다. 예를 들어 2계 텐서를 알아봅시다. 해당 텐서는 성분이 9개 이고 \(T_{xx}, T{xy}, \cdots, T_{zz}\) 입니다. 텐서가 변환할 때 \(R\)이 두번 곱해지는데 식으로 보면 다음과 같습니다.
\[\begin{align} \bar{T}_{xx} &=R_{xx}(R_{xx}T_{xx} + R_{xy}T_{xy} + R_{xz}T_{xz}) \\ &+ R_{xy}(R_{xx}T_{yx} + R_{xy}T_{yy} + R_{xz}T_{yz}) \\ &+ R_{xz}({R_xx}T_{zx} + R_{xy}T_{zy} + R_{xz}T_{zz}), \cdots \\ \end{align} \tag{26}\]물론, 텐서를 표현할 때 매번 이렇게 적을 순 없습니다. 이것이 2계텐서임에도 성분이 9개나 되니까요. 이번에도 한줄로 이쁘게 적어봅시다.
\[\bar{T}_{ij} = \sum_{k=1}^3 \sum_{l=1}^3 R_{ik}T_{kl} \tag{27}\]저희는 2계 텐서에서 다루어 보았습니다. 일반적인 n계 텐서에선 성분이 \(3^n\)개가 되며, 변환할 때 \(R\)의 개수가 n개가 붙게 됩니다. (2계에서는 \(R\)이 두 개씩 곱해졌듯이요.) 이와 같은 체계에서 보면 벡터는 1계 텐서이고 스칼라는 0계 텐서가 되겠네요.
벡터 미분
저희는 벡터의 기본적인 개념을 배웠습니다. 이제부터 벡터의 미분에 대해서 알아보겠습니다.

Leave a comment